哈夫曼树与哈夫曼编码

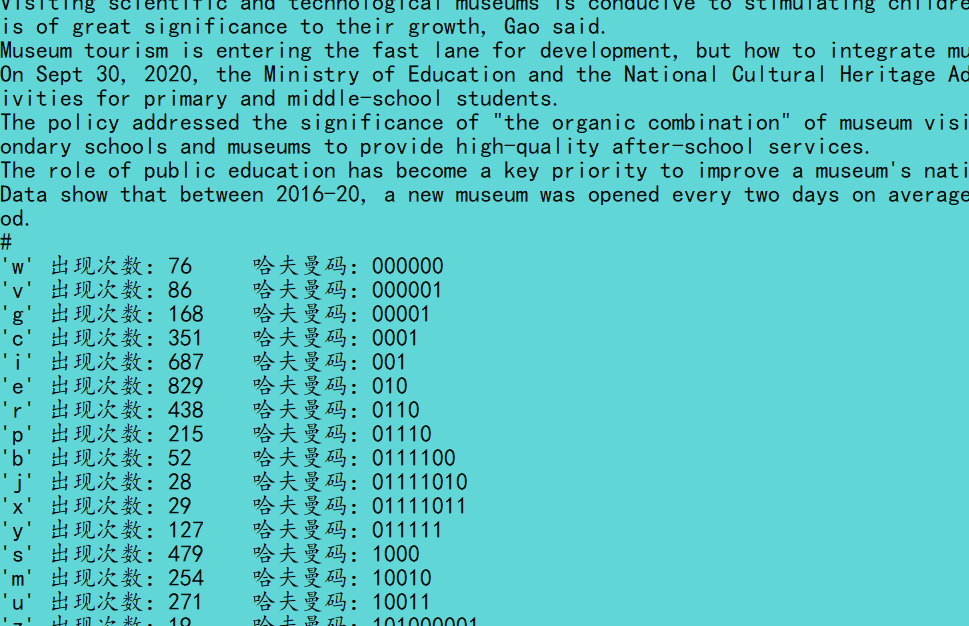
哈夫曼树的作用：哈夫曼树是为解决哪种问题发明的

哈夫曼树的构建原理：哈夫曼树详解

下面浅谈我个人对哈夫曼树的理解及其实现：

阅读网上的哈夫曼树构造方法后，可以发现这是一个重复的过程：提取森林中权值最小的两棵树，并将它们组成新树，再将这个新树再次放入森林，然后重复以上步骤。既然是重复步骤，那么就可以递归实现（实际上，递归也是最易懂，最优雅的方法）。图解如下：

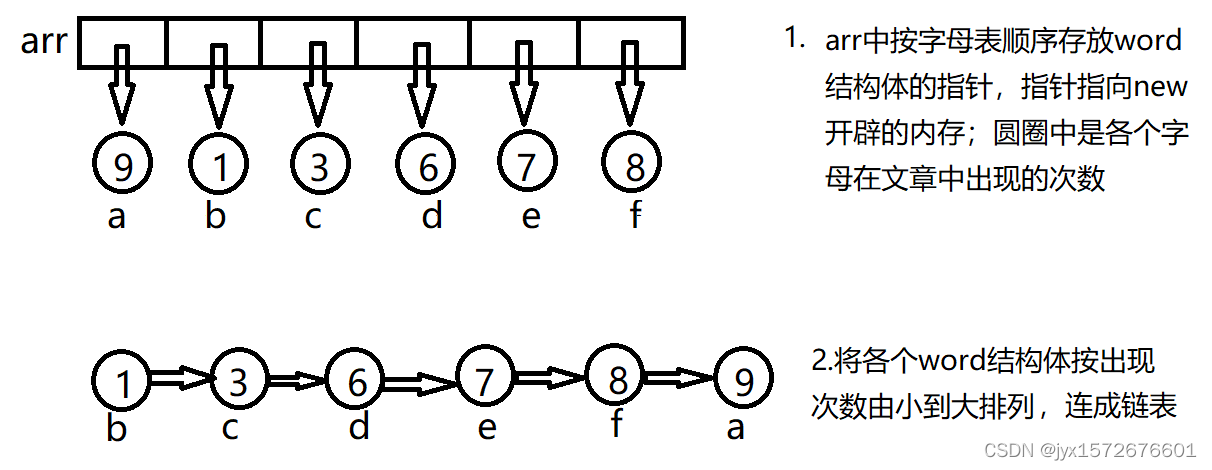
3. 把链表第一个（b）和第二个节点©分别作为新根节点new_root的左右孩子，new_root的权值等于左右孩子权值之和，然后将new_root的权值和第三个(d)及其后面的节点权值依次比较，直到找到一个比new_root权值大的节点（找不到则放最后），并把new_root节点插入到此节点之前；重复上述步骤，图解如下：

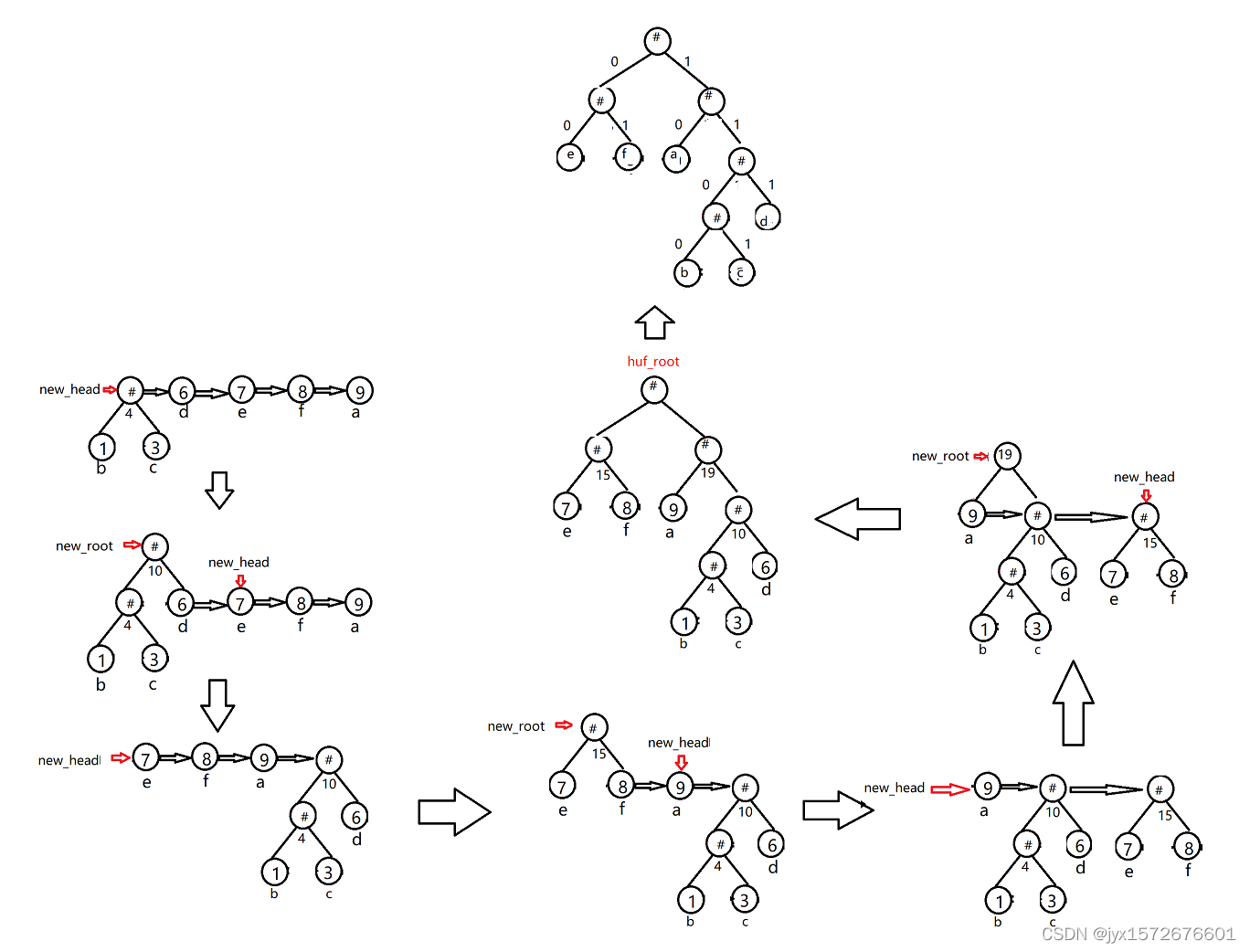
4. 最后把左孩子的权值改为0，右孩子权值改为1，然后遍历树，对各个字母进行编码代码实现如下：

#include<iostream>
using namespace std;
struct huf_tree
{
	char data;//字母或数字
	int weight;//权重
	huf_tree* left;//左孩子
	huf_tree* right;//右孩子
	huf_tree* rlink;//右节点
	string code;//哈夫曼编码，注意用string更方便！易于递归直接string相加
};
struct words//临时的结构体
{
	char letters;
	int counts;//字母or数字的出现次数
};
huf_tree* cre_huf_tree(huf_tree*, int);//建立哈夫曼树
void ini_lett_arr(words**);//初始化字符的结构体指针数组
void essay_data(words**);//提取文章中的字母出现次数,并存入各个字母对应的结构体
huf_tree* cre_link_list(words**);//创建哈夫曼树（递归创建）
void huf_coding(huf_tree* root,string);//编码（递归）
void dis_code(huf_tree* root);//展示各个字母的码值（递归遍历）
int main()
{
	int n = 36;//26个字母+10个数字
	words* letter_arr[36]; //开一个指针数组
	ini_lett_arr(letter_arr);//初始化字母数组（临时，用以排序）
	essay_data(letter_arr);
	huf_tree* head = cre_link_list(letter_arr);
	huf_tree* root = cre_huf_tree(head, n);
	root->code = "";
	huf_coding(root,"");
	dis_code(root);	
}
 
 
void ini_lett_arr(words** arr)
{
	for (int i = 97; i <=122; i++)//将arr数组0-25设置为存放a-z的小写字母的words结构体
	{
		arr[i-97] = new words;//分配实体空间
		arr[i - 97]->letters = i;
		arr[i - 97]->counts = 0;
	}
	for (int i = 48; i <=57 ; i++)//ASCII码48-57对应字符0-9,分别存入arr[26]-arr[35]
	{
		arr[i - 22] = new words;
		arr[i - 22]->letters = i;
		arr[i - 22]->counts = 0;
	}
}
huf_tree* cre_huf_tree(huf_tree* head, int n)
{
	huf_tree* new_root = new huf_tree; //开辟实体空间
	if (n == 2)//递归结束的条件：当link_list中只有两个节点，则进行以下操作后返回
	{
		new_root->right = head->rlink;
		new_root->left = head;
		new_root->data = '#';
		new_root->weight = new_root->right->weight + new_root->left->weight;
		return new_root;
	}
	huf_tree* new_head = head->rlink->rlink;
	huf_tree* temp = new_head;
	new_root->right = head->rlink;
	new_root->left = head;
	new_root->data = '#';
	new_root->weight = new_root->right->weight + new_root->left->weight;
	head->rlink->rlink = NULL;
	head->rlink = NULL;
	int step = -1;//注意，step设置为-1而不是0！由于没有前驱指针（只有后驱指针rlink）,故把A插入BCD中C和D之间，需要把temp停在B而不可停在D！
	if (new_root->weight < new_head->weight)
	{
		new_root->rlink = new_head;
		new_head = new_root;   //如果新产生的根节点权重小于新的头节点，那么此根节点仍然作为链表的头节点；
	}
	else if (new_root->weight == new_head->weight)
	{
		new_root->rlink = new_head->rlink;
		new_head->rlink = new_root;
	}
	else  //否则将产生的根节点插入到链表合适的位置（权值仍从小到达排列）
	{
		while ((temp != NULL) && (new_root->weight > temp->weight))//第一个条件temp!=NULL很重要
		{
			step++;
			temp = temp->rlink;
		}
		temp = new_head;
		for (int i = 0; i < step; i++)
		{
			temp = temp->rlink;      //将temp移动到要插入位置的前一个节点
		}
		new_root->rlink = temp->rlink;
		temp->rlink = new_root;
	}
	return cre_huf_tree(new_head, n - 1);//此处是最关键也是最难想到的：将最终生成的根节点一路向上传回给主函数！这招很帅
}
void essay_data(words** arr)
{
	cout << "输入文段(以'#'结尾):" << endl;
	char letter = getchar();                      //这里将所有的字符存入缓冲区，下面的while依次读取
	while (1)
	{
		if ( letter >= 97 && letter <= 122)//小写字母
		{
			arr[letter - 97]->counts++;
		}
		if (letter >= 48 && letter <= 57)//数字
		{
			arr[letter - 22]->counts++;
		}
		if (letter >= 65 && letter <= 90)
		{
			arr[letter + 32 - 97]->counts++;//把大写字母转为小写并存入
		}
		letter = getchar();
		if (letter == '#')
			break;
	}
}
huf_tree* cre_link_list(words** arr)
{
 
	for (int i = 0; i < 35; i++)          //冒泡排序，从小到大；36个字母，排35次即可
	{
		for (int k = 0; k < 35 - i; k++)  
		{
			if (arr[k]->counts > arr[k + 1]->counts)
			{
				swap(arr[k], arr[k + 1]);//用库中的swap()交换指针的位置
			}
		}
	}
	huf_tree* head = new huf_tree;//为树节点开辟实体空间
	head->weight = arr[0]->counts;
	head->data = arr[0]->letters;
	head->right = head->left = NULL;
	huf_tree* temp_head = head;
	for (int i = 1; i < 36; i++)
	{
		huf_tree* huf_node = new huf_tree;
		huf_node->weight = arr[i]->counts;
		huf_node->data = arr[i]->letters;
		huf_node->left = huf_node->right = huf_node->rlink = NULL;
		temp_head->rlink = huf_node;
		temp_head = temp_head->rlink;
	}
	return head;
}
void huf_coding(huf_tree* root,string code)
{
	if (root->right==NULL || root->left==NULL)//实际上，如果right=NULL，则left必定也为NULL
	{
		return;
	}
	root->left->code = code + "0";
	huf_coding(root->left,root->left->code);      //递归需要注意顺序
 
	root->right->code = code + "1";
	huf_coding(root->right,root->right->code);
}
void dis_code(huf_tree* root)//递归遍历
{
	if (root == NULL)
		return;
	if (root->data >= 97 && root->data <= 122&&root->weight!=0)//数字出现很少，所以这里没有加数字，可以自己加上去
	{                                                         //只显示有权重的字符，没出现过的不显示
		printf("'%c' 出现次数：%-4d   哈夫曼码：", root->data, root->weight);
		cout << root->code << endl;
	}
	dis_code(root->left);
	dis_code(root->right);
}