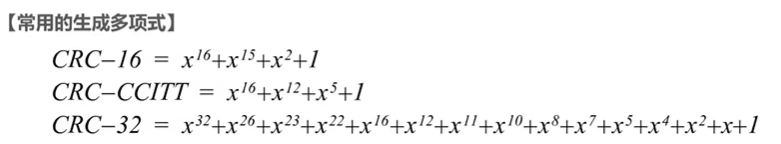差错检测和纠正技术
虽然将本节放入链路层专栏,但需要知道,差错检测和纠正技术不单单出现在链路层,传输层也有此技术的应用,比如 TCP/UDP 中的校验和。校验和主要用于传输层,奇偶校验和循环冗余检测(CRC)则主要用于链路层。
校验和
校验和(Checksum) 是一个端到端的校验方式,由发送端计算,然后由接收端验证,如果接收方检测到校验和有差错,则报文会被直接丢弃 。其目的是为了发现首部和数据在发送端到接收端之间发生的任何改动。UDP 可选择使用校验和,而 TCP 则强制使用校验和 。CheckSum 不同领域可能采用不同算法,算法存在细微差别,且覆盖区域也不同:
-
IP校验和:IP 首部
-
ICMP校验和:ICMP 首部 + ICMP 数据
-
UDP、TCP校验和:首部 + 数据 + 伪首部
伪首部并非 TCP&UDP 数据报中实际的有效成分,它是一个虚拟的数据结构,其中的信息是从数据报所在 IP 分组头的分组头中提取的,既不向下传送也不向上递交,而仅仅是为计算校验和 。伪头部 = 源 IP 地址 + 目的 IP 地址 + 8 位协议 + 16 位 UDP 长度,通过 伪头部+UDP头部+应用层数据,就可以检测出网络层(被递交到错误主机),传输层(被递交到错误进程),应用层(应用数据错误)的比特错误。
下面以 UDP 校验和举例(TCP类似)。
一.计算校验和:
-
把校验和字段设置为 0 (下一步计算时,会包含此部分,所以必须设置为零)
-
把需要校验的数据看成以 16 位为单位的数字组成,依次进行 二进制反码求和
-
把得到的结果存入校验和字段中
另外注意:
- UDP、TCP 数据报的长度可以为奇数字节,因为计算时是 16 位为单位,所以此时计算校验和时需要在最后增加一个填充字节 0 (只是计算校验和用,不发送出去)。
- 二进制反码求和,就是先把这两个数取反,然后求和,如果最高位有进位,则向低位进 1 。先取反后相加与先相加后取反,得到的结果是一样的,因此实现代码都是先相加,最后再取反。

二.检验校验和:
把需要校验的内容(包括校验和字段)看成以 16 位为单位的数字,依次进行二进制反码求和,如果结果是0表示正确,否则表示错误 。
三.实现代码:
1 | static inline uint16_t check_sum(const uint16_t *buffer, int size) |
为什么要用反码计算校验和?
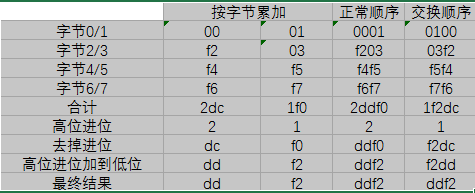
因为使用反码计算就可以避免依赖系统的字节序(大小端) 。即无论你是发送方计算机或者接收方检查校验和时,都不要调用htons或者ntohs,直接通过上面的算法就可以得到正确的结果。用反码求和时,交换16位数的字节顺序,得到的结果相同,只是字节顺序相应地也交换了;而如果使用原码或者补码求和,得到的结果可能就不同。举例如下:
可见,使用反码进行校验和计算,不同字节序所得结果相同。
UDP可选校验和:
UDP 协议可以不选择使用校验和。在这种情况下,发送前 CheckSum 字段全部填充 0 ;如果在 UDP 发送方决定使用 CheckSum 的情况下计算出其值全为0,则在发送前将其全改为 1;注意,这这并不会产生混淆,因为 CheckSum 有可能被计算为全 0 ,但不可能被计算为全 1 (这意味着 CheckSum 覆盖的数据全为 0 ,这是不可能的)。
奇偶校验
奇偶校验用来检测数据传输过程中是否发生比特错误,是众多校验码中最为简单的一种。采用何种校验是事先规定好的 。通常专门设置一个奇偶校验位 ,用它使这组代码中“1”的个数为奇数或偶数。若用奇校验,则当接收端收到这组代码时,校验“1”的个数是否为奇数,从而确定传输代码的正确性,偶校验同理。
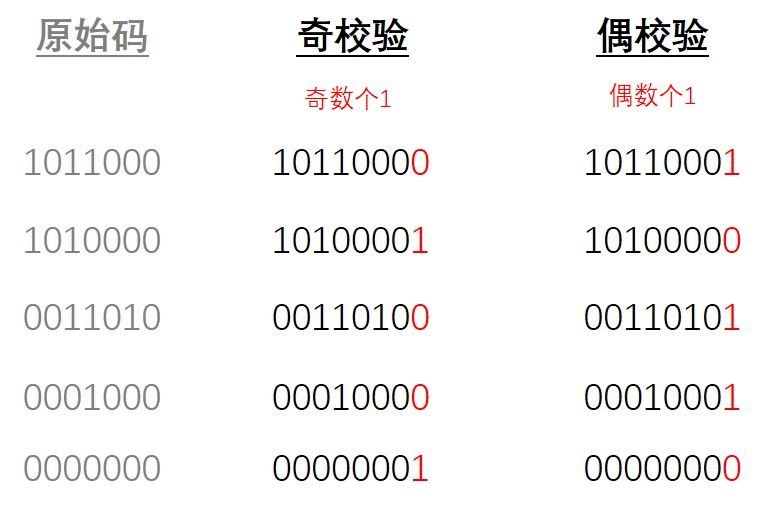
上图中直接将校验位放在了原始字节流的末尾,但实际上通常专门设置一个奇偶校验位。
计算原理:
如果事先规定了采用奇校验,则发送方利用校验位将 数据+校验位 中的 1 的个数调整为奇数个(如上图),接收方收到分组后检验 数据+校验位 的 1 的个数,如果为奇数个,则 基本 能够说明数据没有发生错误,反之 一定 出错。偶校验同理。
万一校验位本身出错呢?
目前笔者没有了解到此问题的解决方案,但需要知道的是,相对于数据而言校验位本身占的位数极少,本来一个分组发生比特错误的概率就极少,而错误发生在校验位而非数据位的概率就更加少了,所以并不用很担心此问题。即使发生错误,链路层和传输层也提供 ARQ 协议来保障数据的正确性。
当出错比特数为偶数,此方法不就失效了吗?
是的,奇偶校验只能检测到出错比特数为奇数的情况,一旦为偶数,就无法检测出错误。但需要知道的是,在某些可靠性较高的链路上(如,以太网)发生比特错误的概率是很小的,而同一个分组中发生多个比特错误的概率则是极小的,在这种情况下,单个奇偶校验位应该是足够的。然而即使如此,测量已经表明差错经常以“突发”的方式聚集在一起,而不是独立的发生,使用单比特奇偶校验保护的一帧中,未检测差错的概率达到了 50%,所以显然我们需要更健壮的差错保护方式。下面我们提供三种方式来提高其健壮性:
-
为每 N 个字节设置一个校验位。比如有 1000 字节的数据,每 100 字节设置一个校验位,则需要总共 10 个校验位。只有在连续的 100 个字节中同时出现多个比特错误才可能导致校验失败,这再次大大减少了失误发生的概率。(此方法为笔者推测,仅供参考)
-
二维奇偶校验: 将数据的 N 个比特划分为 D 行 D 列,对每行和每列都计算校验位。一旦某处发生错误,那么其行/列校验位都会发生变动,因此接收方不仅可以检测的错误的发生,还能定位错误并将其纠正!
需要注意的是,并非任何差错情况都能够纠正(但都可检测到),只要一个分组中出现多个比特差错,就无法纠正。原因是,假设发生两个比特错误,则再上图中就会有三条或四条线,对应三个或四个交点,而只发生了两处错误,所以无法准确定位。
-
汉明码: 汉明码(海明码)在上世纪 40 年代早早地就诞生了,不过直到今天的 ECC 内存里面,我们还在使用这个技术方案,而海明也因为海明码获得了图灵奖。汉明码与二维奇偶校验类似,也属于多重奇偶校验。汉明码不仅可以验证数据是否有效,还能在数据出错的情况下指明错误位置(仅发生一处错误时)。下面我们详细了解其计算方法。
汉明码计算方法
冗余位: “冗余位”是一种二进制位,它被用来添加到需要传输的数据信息中,以侦测数据在传输过程中发生的丢失或者改变。汉明码需要多少个冗余位?答案如图:

对于 7 位有效数据,汉明码需要 4 位冗余码进行纠错,所以最早的汉明码又叫 7-4 汉明码 。下面的讨论采用 7-4 方式且使用 奇校验 进行举例说明 。
编码方式:
-
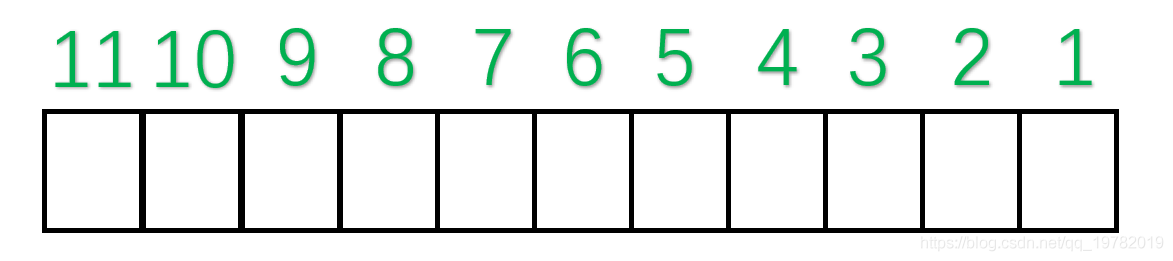
为方便讨论,对比特位进行编号。7个有效位,4个冗余位,一共11位。
-
汉明码对于奇偶校验位的位置有特殊要求 :所有2的幂次位(2^0=1,2^1=2,2^2=4,2^3=8……)作为“奇偶校验位” ,因此,第1位,第2位,第4位,第8位为奇偶校验位,其他的7位为数据位。
-
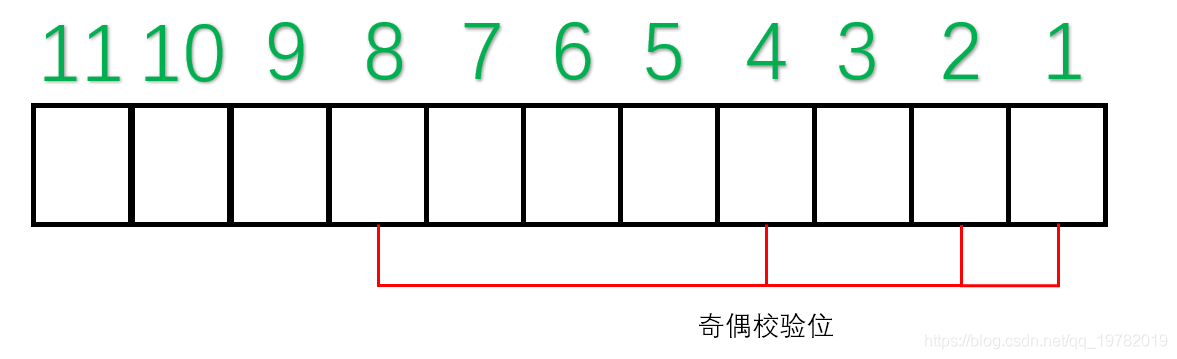
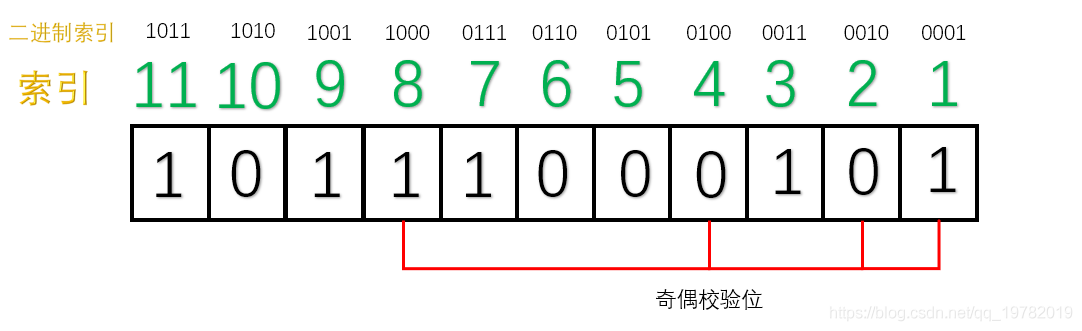
表示出索引的二进制:
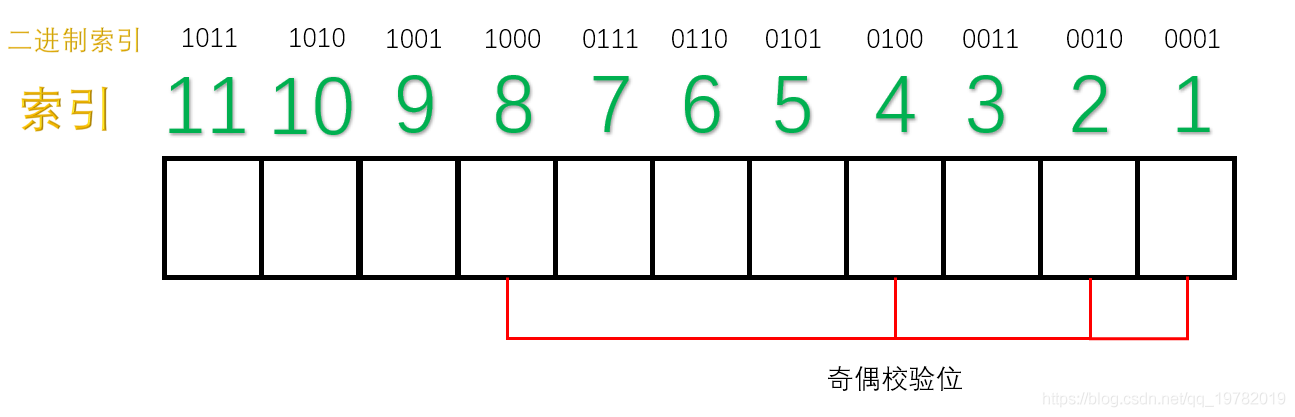
并对索引进行分类:从右往左(低位往高位)数 ,第一位是“1”的索引有:1011, 1001, 0111, 0101, 0011, 0001;于是这些位置由第一个校验码管理:
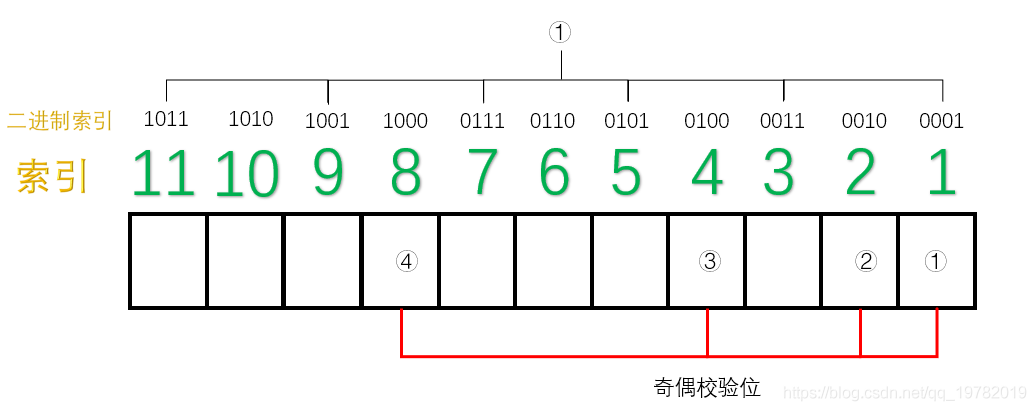
第二位是“1”的索引有:1011, 1010, 0111, 0110, 0011, 0010;于是这些位置由第二个校验码管理:
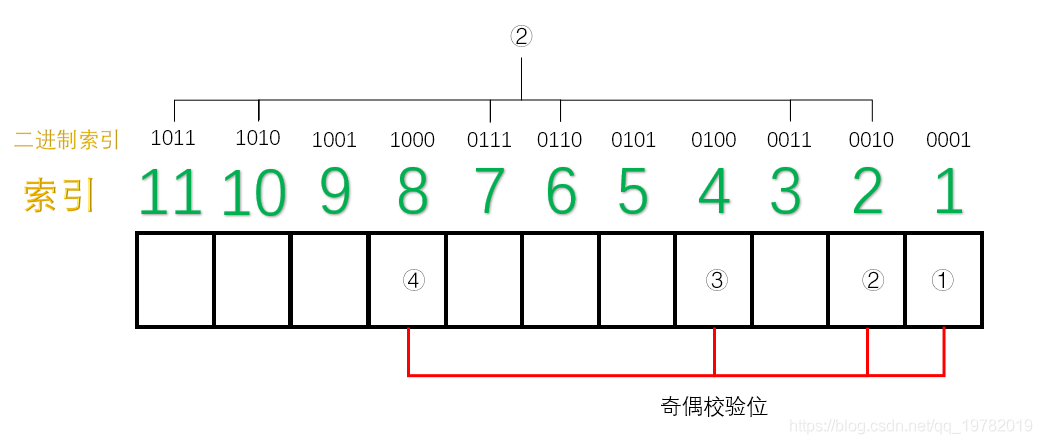
其他两组同理。 -
填充数据位:
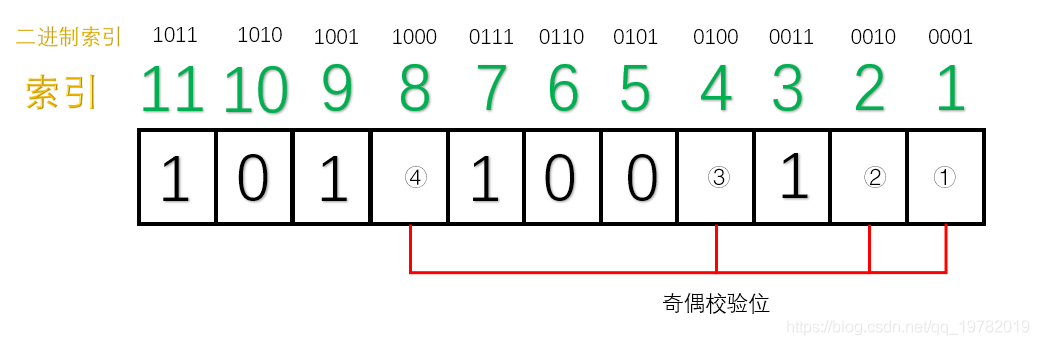
填充冗余位:第一组(1,3,5,7,9,11位):1 的个数为 4 个,偶数个,因此①号应该为 1(采用的是奇校验);类似的,得出其他冗余位:
构造完毕。
汉明码的纠错机制:
汉明码通过检查每一小组的“奇校验”,来确定是否发生了错误。
首先第一组(1,3,5,7,9,11位):1 的个数为 6 位,不再是奇数个了,因此,我们可以断定,这一组中肯定有某个数据发生了错误,但不能确定是哪一位上发生了错误。为了达到“奇校验”,我们必须补 1 个 1 来达到奇数个 1。
接下来,我们检查第二组(2,3,6,7,10,11) ,1的个数为3位,仍然满足“奇校验”,因此我们也可以断定这一组中没有任何一位数据发生了改变。所以,我们只需要补 0。
我们继续检查第三组(4,5,6,7),1 的个数为 2,不在满足“奇校验”,因此,我们可以断定,这一组中也有数据发生改变。为了达到“奇校验”,我们必须补 1 个 1 来达到奇数个1。
我们检查第四组(8,9,10,11位),1 的个数为 3 位,满足“奇校验”,因此没有发生改变。所以我们只需要补0。
如下图所示:
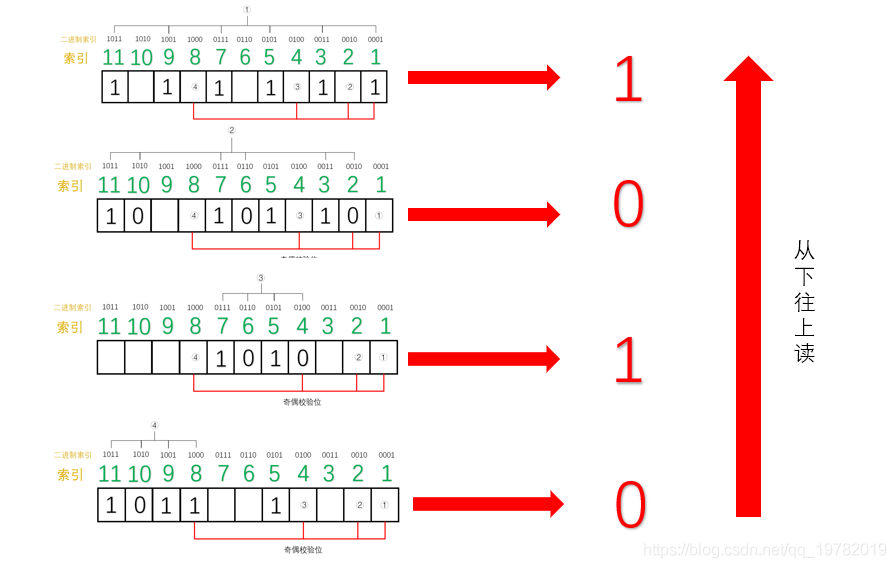
我们发现,最后得出来的二进制数是:0101 ,我们会神奇地发现,0101 就是十进制 5 的二进制表现,因此,我们可以准确的知道,5号位上发生了数据的改变,我们只要对 5 号位进行置反操作即可。最后,接收方就可以修改成为正确的数据。
二维奇偶校验与汉明码谁略胜一筹?
笔者提供一个思路(仅供参考):对于 10000 字节的数据而言,二维奇偶校验需要 200 个冗余字节(行100,列100);而汉明码则最少只需要约 14 个字节(通过上面的公式计算得出),所以在有效利用率上,汉明码更胜一筹。但显然二维奇偶校验的思路更加简单。
循环冗余校验(CRC)
CRC 循环冗余校验属于检错码,只能检测出现了错误,但无法纠正错误 。与 CRC 循环冗余校验类似的,还有奇偶校验,但是 CRC 漏检率更低 ,因此在实际应用中更为重要。CRC 常用于数据链路层的错误检测,通常在帧尾添加 CRC 校验码。
CRC 校验流程概述 :发送方在原始数据的基础上,加上 CRC 校验码,组成新的发送数据;然后接收方对收到的 原始数据 + 校验码 进行校验,判断数据在传输过程中是否出现错误,若出错则丢弃,并反馈相应信息。
CRC校验步骤:
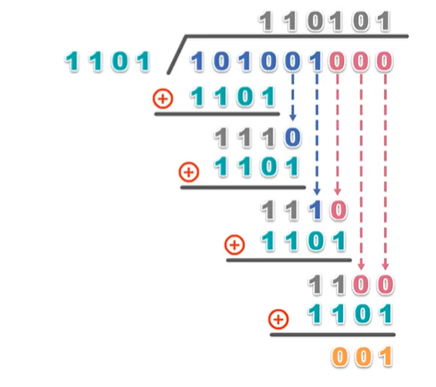
发送方追加校验码:
- 假设原始数据是:
101001 - 生成待追加的校验码,需要使用一个生成多项式G(x)(收发双方事先约定) ,例如 G(x) =
- 构造被除数:原始数据 + 生成多项式最高次项个0,即:
101001000 - 除数:除数实际上就是生成多项式的系数,G(x) 展开得到 : G(x) = 即
1101 - 两数相除得余数,并进行补位(补到与生成多项式最高次项一致) ,即得到校验码。但是,这里的除法跟常规除法并不相同,本处使用的是模2除法 ;常规除法在上下两行数进行运算时,使用的是减法运算,而这里使用的是异或运算。通过上述运算,得到校验码
001,添加到原始数据之后,得到最终发送数据为101001001
接收方进行校验:
- 继续接前文,假设收到的数据为
101001001 - 接收方对该数据做除法,除数仍然是之前使用的多项式的系数
1101,过程如下:
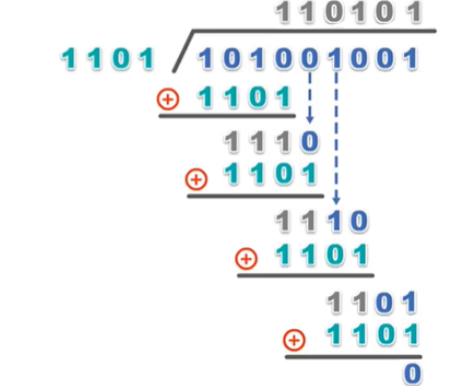
若余数不为0,则表明发生比特错误 。
另外,在实际使用 CRC 时,采用的生成多项式更为复杂,从而确保较低的漏检率:
总结
接收方检测和纠正差错的能力被称为 前向纠错(Forward Error Correction, FEC) 。在网络环境中,FEC 可以单独应用,也可以与链路层的 ARQ 技术一起应用。FEC 技术具有很高应用价值,因为它们可以减少重发次数,避免了潜在的往返时延,这对于实时网络应用尤其重要。
参考资料:伪首部,校验和计算器,校验和计算方法,校验和计算原理,汉明码通俗讲解,汉明码-百度,CRC计算流程详解,CRC代码实现,《计算机网络自顶向下》
.PNG)