堆与堆排序

完全二叉树

什么是完全二叉树？
如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是 满二叉树 ；也可以这样解释：如果二叉树中除了叶子结点，每个结点都有左右两个子树，则此二叉树称为满二叉树。如下两个树都是满二叉树：

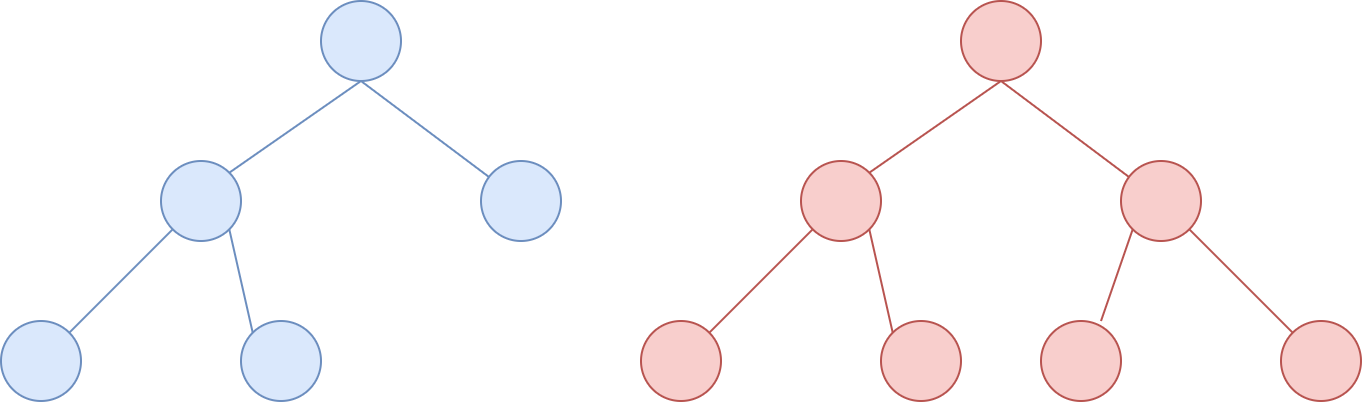
而 完全二叉树 的定义为：如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。也可以这么定义：一棵深度为 k 的有 n 个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为 i（1≤i≤n）的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。如下两棵树就是完全二叉树：

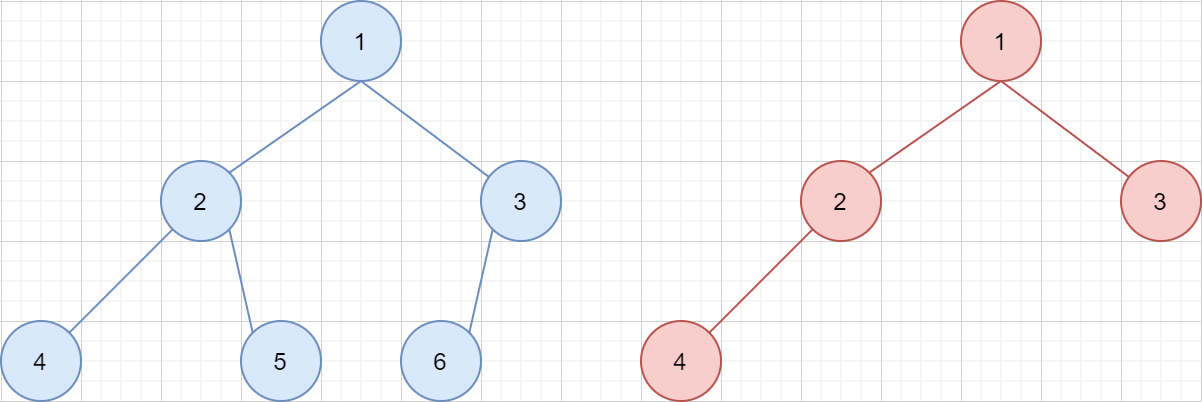
完全二叉树的表示
二叉树的存储结构有两种，分别为顺序存储和链式存储。这里我们采用顺序存储。完全二叉树的顺序存储，仅需从根节点开始，按照层次依次将树中节点存储到数组即可。 图示如下：

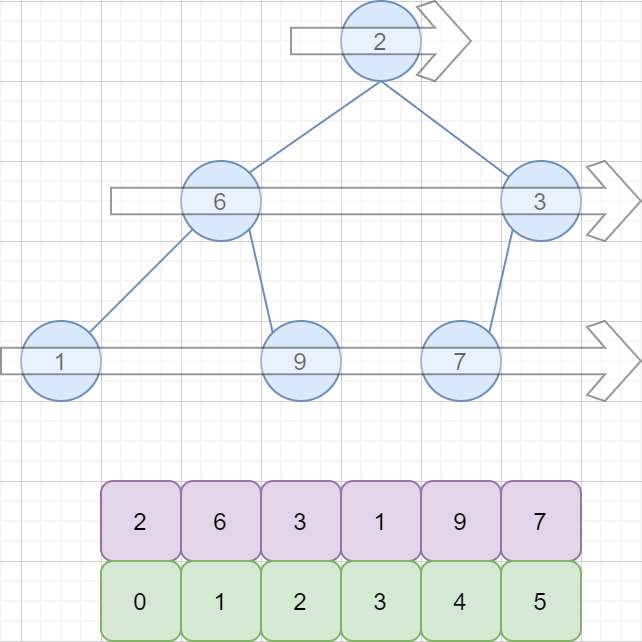
以数组下标 i 表示节点的位置，可得以下公式：

节点i的父节点=[(i-1)/2] ，[ ] 表示向下取整。比如上图中值为 9 的节点，其下标为 4，[ (4-1) / 2 ] = 1，所以其父节点位置为 1，值为 6。
节点i的左孩子=2*i+1 ，节点i的右孩子=2*i+2 。

堆

堆的定义
定义1：堆是一种特殊的完全二叉树，其每一个节点的值都是在以该节点为根节点的树中最大(小)的值。定义2：堆中某个结点的值总是不大于或不小于其父结点的值；如下图：

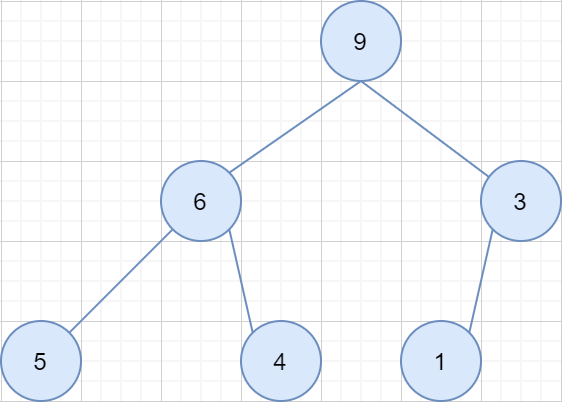
堆的作用

堆的重要作用是用来实现优先级队列 。什么是优先级队列呢？优先级队列（priority queue）是多个元素的集合，每个元素都有一个优先权；优先级队列的出队顺序总是按照元素自身的优先级；换句话说，优先级队列是一个自动排序的队列 。对优先级队列执行的操作有 （1）查找（2）插入一个新元素（3）删除 ；一般情况下，查找操作用来搜索优先权最大（即数值最大或最小）的元素，删除操作用来删除优先权最大的元素。 优先级队列是用来处理动态问题的，需要频繁入队和频繁把优先级最高的元素出队。
小伙伴们一定会产生这样一个疑问：既然堆是用来动态获取集合中的最大值或最小值，那为什么不直接将集合进行排序呢？排序后不也能很快找到最大或最小值吗？没错，当数据量小时，可以直接使用排序，但当数据量很大且动态加入数据时 ，数组中每次进来一个新的数据，你难道得全部重新排序一下吗？显然这样效率极低，此时就需要用到堆。建好堆后，数据动态的插入和删除，时间复杂度都为O(logn)；查询最大/小值，时间复杂度为O(1)，具体分析见后文。

堆的构建
堆的构建有两种方式：

从上往下构建 ，当数据不是一次性交付时（比如每次只输入一个数)，采用此方式；该方法复杂度为 $O(NlogN)$
从下往上构建 ，当数据一次性交付时，采用此方式构建；该方法复杂度为 $O(N)$ 。复杂度分析见后文。

1.从上往下构建
核心为 heapInsert() 方法。以构建大堆为例：

当加入一个新数字时，heapSize++，将该数字放入数组堆末尾，即 arr[heapSize-1]位置；
接着将 arr[heapSize] 与其父节点进行比较，如果 arr[heapSize] 大于父节点的值，则 swap 此二节点；否则重复 1。
swap 后继续比较该节点与其新的父节点，如果前者大于后者，则再次 swap，如此反复，直到该节点不再大于其父节点。

过程图示如下：

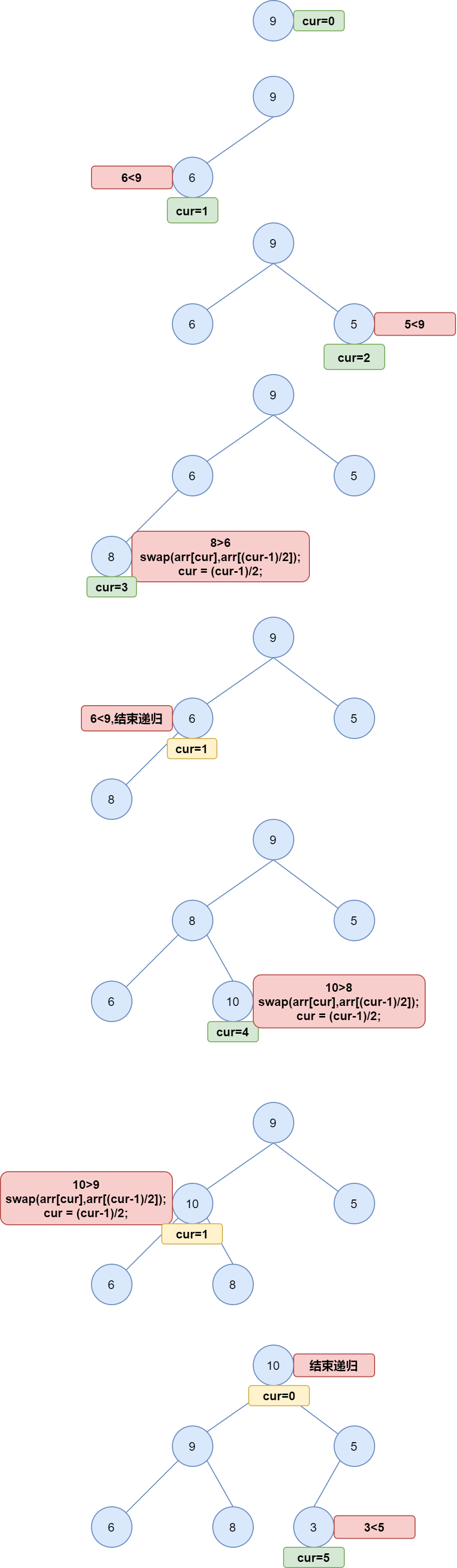
代码如下：

void heapInsert(int* arr,int cur)
{
	if(arr[(cur-1)/2] < arr[cur])//大顶堆
	{
		swap(arr[(cur-1)/2],arr[cur]);
		heapInsert(arr,(cur-1)/2);
	}
}

void createHeap(int* arr,int size)
{
	for(int i=0;i<size;i++)
		heapInsert(arr, i);
}

本方法采用递归实现，也可迭代实现。
如果要改为小顶堆，将第 3 行的 < 改为 > 即可。
注意：第 3 行的 < 不能改为 <=，否则当 cur = 0 时，将会一直重复。
heapInsert() 无需 heapSize，因为是从当前位置往前 swap，而不是往后 swap。

2.从下往上构建
核心为 heaplify() 方法，以构建大顶堆为例：

代码：

void heaplify(int* arr, int cur, int heapSize)
{
	int leftChd = cur * 2 + 1;
	if (leftChd > heapSize-1)
		return;
	int largest = leftChd + 1 < heapSize && arr[leftChd + 1] > arr[leftChd] ? leftChd + 1 : leftChd;
	if (arr[largest] > arr[cur])
	{
		swap(arr[largest], arr[cur]);
		heaplify(arr, largest, heapSize);
	}
}
void createHeap(int* arr,int size)
{
	for (int i = size; i >= 0; i--)
		heaplify(arr, i, size);
}

注意第 6 行代码的作用：如果没有右孩子，那么直接选择左孩子为比较对象；如果有右孩子，则选出左右孩子中最大的那个作为比较对象。

删除堆顶
删除堆顶的步骤很简单：

交换堆顶和堆中最后一个节点。
删除最后一个节点，即缩小堆的大小（heapSize–）

注意，数组 arr 是堆 heap 的物理结构，arr 的大小应大于 heapSize；堆通过 heapSize 的加减进行伸缩。
另外需要注意的是，由于是排序，一次性交付整个待排序的数组，所以堆可以直接在数组首部构建，无需额外空间复杂度；但在其他很多情况下，堆一般可直接由可变长数组（vector）实现；两者原理是一样的。
堆顶调用 heaplify()；

图示如下：

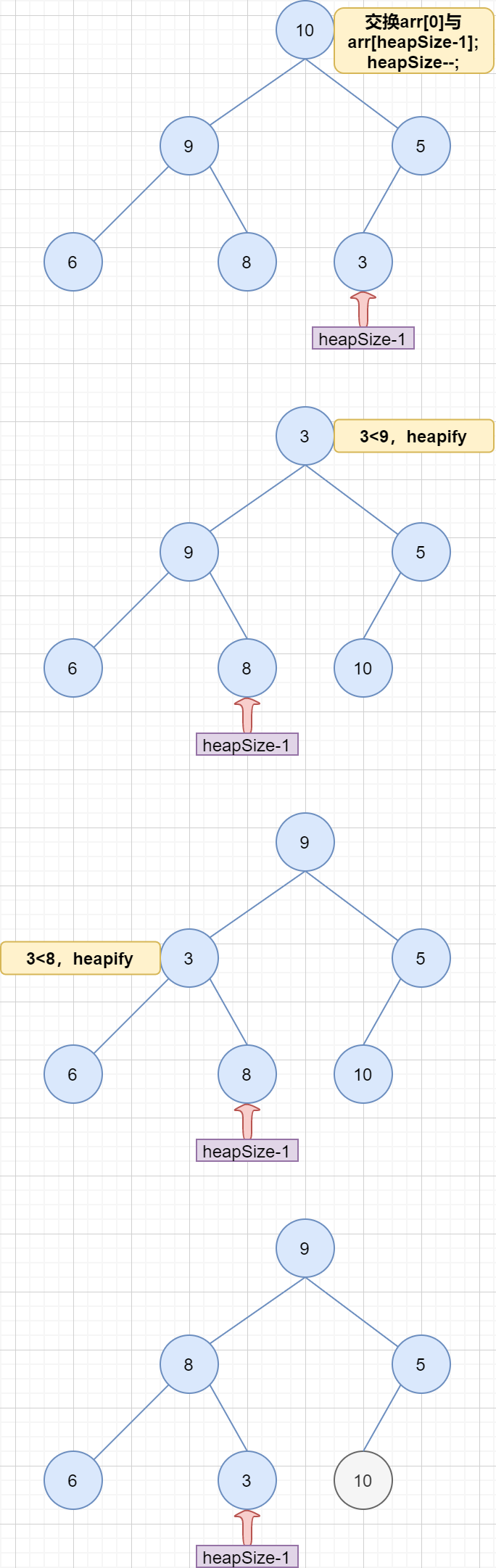
堆排序

堆排序就是不断删除堆顶的过程，每次堆顶都移到数组的 heapSize-1 的位置，所以对于大顶堆，排序结果就应该为升序；对于小顶堆，排序结果就为降序。
代码如下

#include<iostream>
#include<cstdlib>//rand()
#include<ctime>//time()
#include<cstring>//memcpy()
using namespace std;

void swap(int& a, int& b)
{
	int temp = a;
	a = b;
	b = temp;
}
//===================================================================================================
//堆排序
void heapInsert(int* arr, int cur)
{
	if (arr[(cur - 1) / 2] < arr[cur])//大顶堆
	{
		swap(arr[(cur - 1) / 2], arr[cur]);
		heapInsert(arr, (cur - 1) / 2);
	}
}

void heaplify(int* arr, int cur, int heapSize)
{
	int leftChd = cur * 2 + 1;
	if (leftChd > heapSize-1)
		return;
	int largest = leftChd + 1 < heapSize && arr[leftChd + 1] > arr[leftChd] ? leftChd + 1 : leftChd;
	if (arr[largest] > arr[cur])
	{
		swap(arr[largest], arr[cur]);
		heaplify(arr, largest, heapSize);
	}
}

void heapSort(int* arr, int size)
{
	for (int i = size; i >= 0; i--)
	{
		heaplify(arr, i, size);
	}
	//for (int i = 0; i <= size; i++)
	//{
	//	heapInsert(arr, i);
	//}

	for (int i = 0; i < size; i++)
	{
		swap(arr[0], arr[size - 1 - i]);
		heaplify(arr, 0, size - i - 1);
	}
}

复杂度分析

从上向下建堆的复杂度为 $O(NlogN)$ ，原因如下：
$log1+log2+log3+...+logN<NlogN$ ，即复杂度上限为 $NlogN$ 。
$NlogN<log(N+1)+log(N+2)+log(N+3)+...+log2N<Nlog2N$ ，即当 数据倍增 后，复杂度下限仍为 $NlogN$ ，故复杂度为 $O(NlogN)$ 。