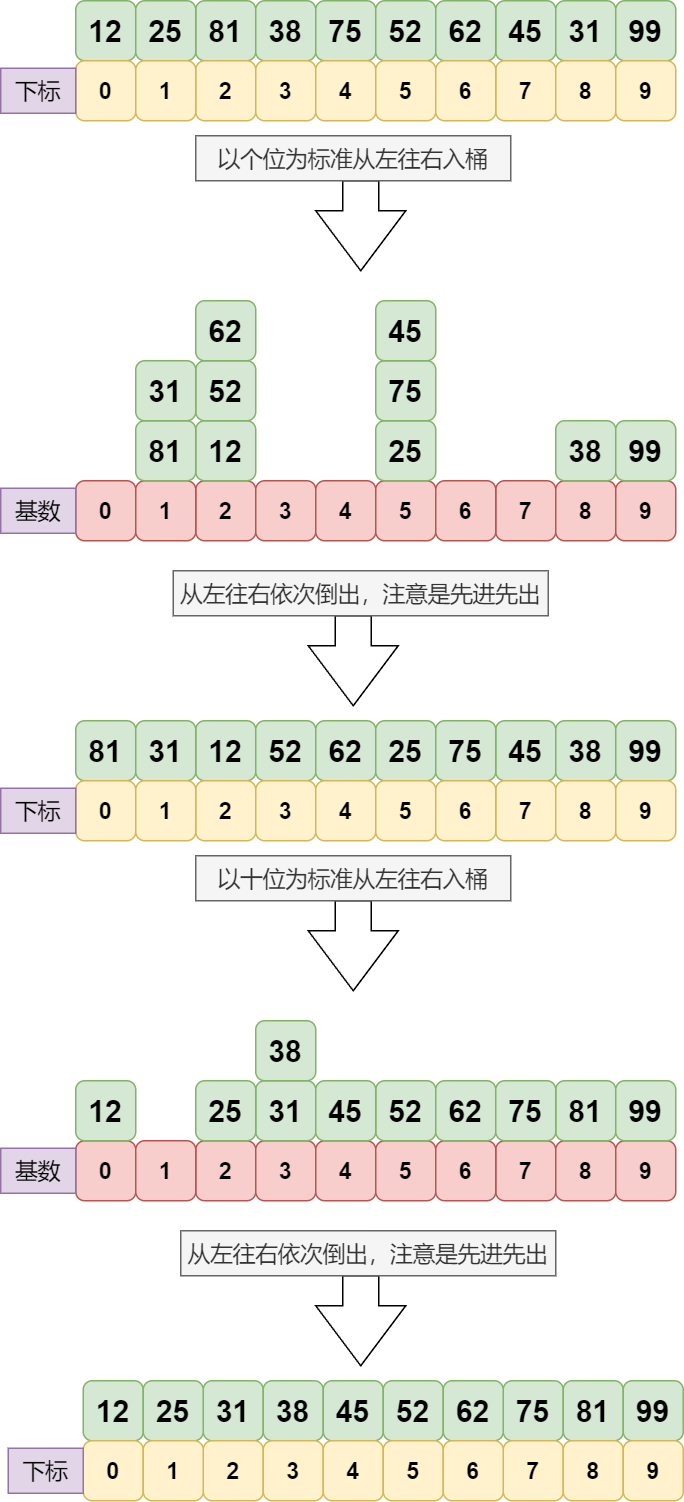
基数排序
算法解析
和计数排序一样,基数排序也是一种 非比较 的排序。其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于它不是基于比较的排序,所以其复杂度突破了比较排序的下限 ,达到了 ,其中 k 是最大数字的位数,N 是待排序数字的个数。基数排序也同样用到了桶的思想,下面我们来看看它是如何进行排序的:
不难看出其排序过程:先以个位数为标准进行排序,在此基础上又以十位数为标准进行排序。这个过程很好理解,就相当于将 10~19 的数分在一组,20~29 的数分在一组,显然前组都小于后组,然后组内又排序,此时由于十位都相同,所以只需比较个位即可。
同时发现,我们需要开辟十个桶(0~9)来完成排序,但这样又耗费了较大的空间。实际上有一种更加优雅的方法,只需要开辟两个数组就能完成基数排序,让我们来看看具体是如何操作的。
然后创建一个 count 辅助数组,并统计个位数字的个数:
然后将 count 数组改成前缀和的形式,得到 count' 数组:
然后我们在 原数组 中从右往左遍历:
- 取出 99
- 其个位数为 9
- 由
count'数组得知个位数小于等于 9 的一共有 10 个数 - 那么这 10 个数将占据数组(按个位排好序后的数组)的 0~9 位置
- 由于是从右往左遍历,所以 99 就占据 0~9 中的最后一个位置,即下标 9 的位置
- 将 99 放入临时数组
tmp[9]位置 count'[9]--
大家可能不理解第 5 步中为什么能得出“99 就占据 0~9 中的最后一个位置”,很简单,因为个位数小于等于 8 的一共有 9 个数,这 9 个数一定将占据数组的 0~8 位置,那就只有剩下标 9 一个位置喽,所以 99 就当然只能占据下标 9 位置。那么为什么说 “由于是从右往左遍历” 呢,这里还不能体现原因,请往下看。
让我们继续,以 45 为例:
- 取出 45
- 其个位数为 5
- 由
count'数组得知个位数小于等于 5 的一共有 8 个数 - 那么这 8 个数将占据数组的 0~7 位置
- 由于是从右往左遍历,所以 45 就占据 0~7 中的最后一个位置,即下标 7 的位置
- 将 45 放入临时数组
tmp[7]位置 count'[5]--
再来,假设依次取到了 75:
- 取出 75
- 其个位数为 5
- 由
count'数组得知个位数小于等于 5 的一共有 7 个数(别忘了上面第 7 步自减了) - 那么这 7 个数将占据数组的 0~6 位置
- 由于是从右往左遍历,所以 75 就占据 0~6 中的最后一个位置,即下标 6 的位置
- 将 75 放入临时数组
tmp[6]位置 count'[5]--
现在让我们回过头来,将注意力放在 45,75,25 这三个数上。由 count' 数组得知,小于等于 4 的有 5 个数,它们将占据 0~4 位置;小于等于 5 的有 8 个数,于是它们只能占据 5~7 位置(0~4 位置被小于等于 4 的数字占据)。那么现在问题是:如何确定 45、75、25 这三个数在 5~7 位置上的相对顺序呢?这就是为什么上面说“由于是从右往左遍历,所以xxx就占据最后一个位置”。还是以 45、75、25 为例,45 是这三个数中最靠右(原数组中)的数,所以在出桶时(参见图1),也就只能位于 5~7 中最后的那个位置喽!理解了这点,第 7 步的自减操作也就迎刃而解了。
以上是对个位的排序,接着还需要进行对十位、百位等高位的排序,就不赘述了,上代码:
1 | int getDigit(int num, int fig) |
算法特性
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大 。
- 时间复杂度 :设数据量为 N、最大位数为 k ,通常情况下 k 相对较小,时间复杂度趋向 。
- 空间复杂度 :非原地排序,且需要借助长度为 N 和 d 的数组
tmp和count。 - 稳定排序
最后笔者将基数排序和快排进行了比较,得到如下结果(Function1是快排,Function2是基数排序):
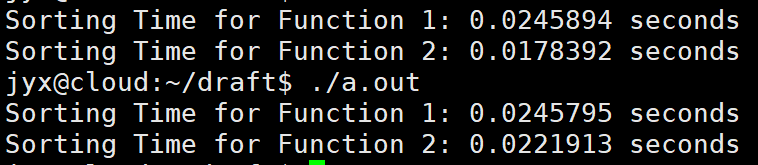
多次比较中,基数排序速度均超快速排序!说明基数排序还是非常强劲的。既然基数排序表现得相当优异,那为什么实际中快速排序却成为了主流算法呢?网上关于这点有很多讨论,参见知乎-链接 。